【机械基础】尺寸链的基础知识，搞设计的必须懂

发布时间:2023/08/05 浏览次数:120 分类:企业新闻分类:行业新闻

基准重合时工序尺寸与公差的确定

1．确定各加工工序的加工余量

2．从最后工序开始，即从设计尺寸开始到第一道加工工序，逐次加上每道加工工序余量，得各工序基本尺寸（包括毛坯尺寸）。

3．除最后工序，其余工序按各自所采用加工方法的加工精度确定工序尺寸公差。

4．按入体原则标注工序尺寸。

一工艺尺寸链

尺寸链定义：

尺寸链：将相互关联的尺寸按一定的顺序联接成首尾相接的封闭图形。
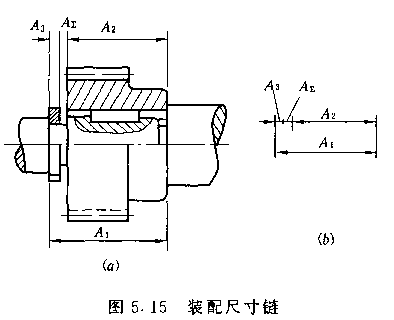
工艺尺寸链：由单个零件在工艺过程中形成的有关尺寸的尺寸链。

尺寸链的组成
1. 环：组成尺寸链的每个尺寸A1 、A2、、A3
2. 封闭环：在加工过程中间接得到的尺寸A2。
3. 组成环：在加工过程中直接得到的尺寸A1 、A3。
增环：其余各组成环不变，此环增大使封闭环增大者。
减环：其余各组成环不变，此环增大使封闭环减少者。

具体判断：给封闭环任选一个方向，沿此方向转一圈，在每个环上加方向，与封闭环方向相同者为减环，相反者为增环。

特点：

1.寸链必须封闭
2．尺寸链只有一个封闭环
3．封闭环的精度低于组成环精度
4．封闭环随组成环变动而变动

作法：
1．找出封闭环
2.从封闭环起，按工件表面上关系依次画出组成环，直到尺寸回到封闭环起，形成一个封闭图形，组成尺寸链的组成环环数应是最少的。
3．相接原则，确定增环、减环。

尺寸链的基本计算

1、尺寸链图中的每一个尺寸都称为链环，所有的链环构成尺寸链。

2、在尺寸链中，能人为的控制或直接获得的尺寸称为组成环。

3、在尺寸链中被间接得到的，当其他尺寸出现后自然形成的尺寸称为封闭环(终结环)。每一个组成环的增大或减小都会使封闭环发生变化，一个尺寸链中只有一个封闭环。

4、某组成环增大而其他组成环不变，会使封闭环随之增大，则此组成环为增环。（与封闭环方向相反的为增环。）

5、某组成环增大而其他组成环不变，会使封闭环随之减小，则此组成环为减环。（与封闭环方向一致的为减环。）

三：计算公式

封闭环的基本尺寸=各组成环的基本尺寸的代数和-增环的基本尺寸之和-减环的基本尺寸之和。

封闭环的最大极限尺寸=所有增环的最大极限尺寸—所有减环的最小极限尺。

封闭环最小极限尺寸=所有增环的最小极限尺寸—所有减环的最大极限尺寸。

封闭环的上偏差=所有增环的上偏差之和—所有减环的下偏差之和

封闭环的下偏差=所有增环的下偏差之和—所有减环的上偏差之和

封闭环的公差=封闭环的最大极限尺寸—封闭环的最小极限尺寸
=封闭环的上偏差—封闭环的下偏差
=增环的公差之和+减环的公差之和
=所有组成环的公差之和

偏差确定：一般根据‘入体’原则

1）组成环为包容面时，下偏差为0，上偏差=公差
2）组成环为被包容面时，上偏差为0，下偏差=公差